정렬 개념
- 정렬은 사용자가 정의한 순서로 데이터를 나열하는 것을 말한다. 사용자가 정의한 순서는 오름차순 / 내림차순일 수도 있고 임의의 조건이 될 수도 있다.
정렬이 필요한 이유
- 데이터를 정렬하면 원하는 데이터를 쉽게 찾을 수 있다. 이진 탐색 트리가 그 예이다.
- 데이터를 정렬하지 않은 값에서 중앙값을 찾으려면 모든 데이터를 확인하고 비교해야 한다. 반면 데이터를 정렬하면 데이터의 값을 보거나 비교할 필요 없이 말 그대로 데이터 전체 크기에서 중간의 값만 찾으면 그 값 자체가 중앙값이 된다.
삽입 정렬
- 데이터의 전체 영역에서 정렬된 영역과 정렬되지 않은 영역을 나누고 정렬되지 않은 영역의 값을 정렬된 영역의 적절한 위치로 놓으며 정렬한다.

- 정렬되지 않은 영역의 맨 앞에 있는 값을 키라고 부른다.
- 삽입 정렬의 과정
- 최초에는 정렬된 영역을 왼쪽 1개, 정렬되지 않은 영역을 나머지로 친다.
- 키와 정렬된 영역의 맨 끝 값부터 거슬러 올라가며 다음 처리를 한다.
- 키보다 크면 해당 값을 오른쪽으로 한 칸 밀어낸다.
- 키보다 작거나 더 이상 비교할 값이 없으면 밀어낸 자리에 키를 넣는다.
- 모든 데이터가 정렬된 영역이 될 때까지 위의 단계를 반복한다.
- 삽입 정렬의 시간 복잡도
- 최악의 경우 O(N^2)
- 최선의 경우 O(N)
병합 정렬
- 정렬되지 않은 영역을 쪼개서 각각의 영역을 정렬하고 이를 합치며 정렬하는 방식
- 이런 방식을 분할 정복 (Divide and Conquer) 이라고 한다.
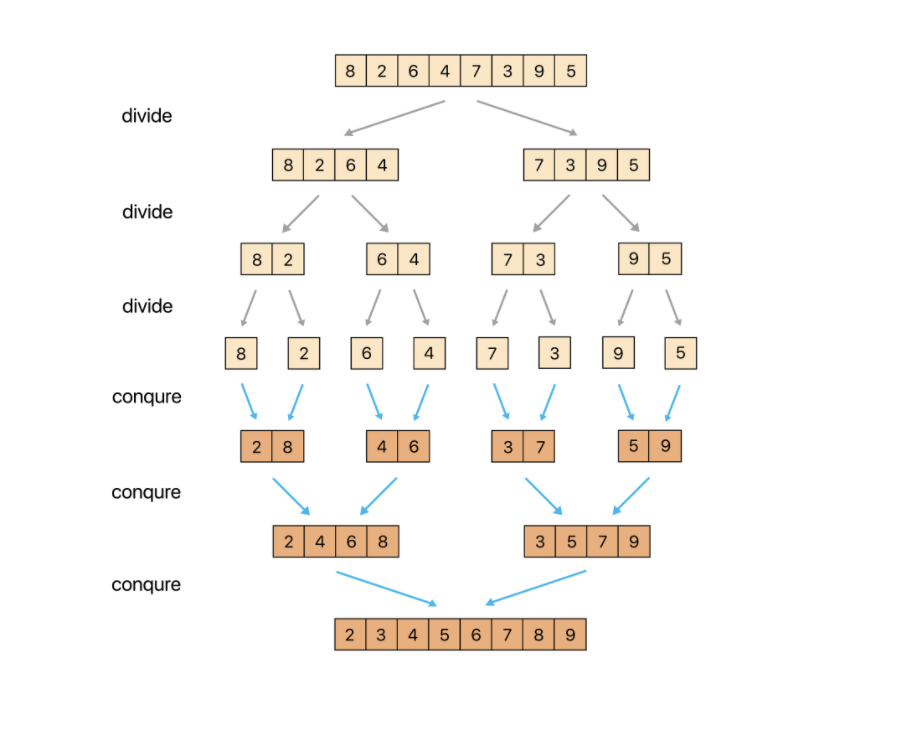
- 이런 방식을 분할 정복 (Divide and Conquer) 이라고 한다.
- 정렬되지 않은 영역이 1칸이 될 때까지 반씩 쪼갠 후 다시 조합할 때 오름차순으로 정렬하며 합친다.
- 병합 정렬에서의 핵심은 ‘병합할 때 정렬하는 부분을 어떻게 구현해야 하는ㄱ?’ 이다.
- 병합 정렬의 과정
- 각 데이터의 첫 번째 원소를 가리키는 포인터를 만든다.
- 포인터가 가리키는 두 값 중 작은 값을 선택해 새 저장 공간에 저장한다.
- 값이 선택된 포인터는 다음 위치의 값을 가리킨다.
- 새 저장 공간에 하나의 데이터가 완전히 저장될 때까지 위 과정을 반복한다.
- 저장할 값이 남은 데이터의 값을 순서대로 새로운 저장 공간에 저장한ㄷ.
- 그러면 새로운 저장 공간에 두 개의 데이터가 정렬된 상태로 저장된다.
- 새로운 저장소에 저장된 값의 개수와 초기에 주어진 데이터에 들어있는 값의 개수가 같을 때까지 과정 1, 2를 반복한다.
- 각 데이터의 첫 번째 원소를 가리키는 포인터를 만든다.
📄
포인터라는 개념?
말 그대로 특정 배열의 원소를 가리키기 위한 화살표 같은 것.
- 병합 정렬의 시간 복잡도
- 병합 정렬의 동작은 분할과 정복(결합)으로 나눠진다.
- 분할은 배열을 계속 반으로 나누는 과정이고, 더 이상 나눌 수 없을 때까지 반복하므로
- log_2N번 진행한다.
- 정복은 다시 병합하며 정렬하는 과정이기 때문에 데이터가 N개면
- N번 진행하여 병합한다.
- 분할과 정복을 종합하면 log_2N번의 나누기와 N번의 병합을 수행하므로 총 Nlog_2N번 연산한다.
- 다만, 시간 복잡도에서는 밑이 2인 로그는 생략하므로 O(NlogN)이라고 할 수 있다.
힙 정렬
- 힙이라는 자료구조를 사용해 정렬한다.
- 따라서 힙 정렬은 힙 자료구조가 무엇인지 먼지 알아야 한다.
- 힙 정렬을 하기 위해서는 먼저 주어진 데이터로 힙을 구축해야 한다.
- 힙은 특정 규칙이 있는 이진 트리이다. 규칙에 따라 최대 힙, 최소 힙으로 나뉠 수 있다.
- 최대 힙은 부모 노드가 자식 노드보다 크고, 최소 힙은 부모 노드가 자식 노드보다 작다.힙이란?

- 왼쪽의 최대 힙을 보면 부모 노드는 항상 자식보다 크다. 반대로 오른쪽의 최소힙은 부모 노드가 항상 자식보다 작다.
힙 구축 방법 : 최대힙
- 최대힙과 최소힙은 힙을 구성하는 규칙만 다르고 나머지는 모두 동일하다.
- 최대힙을 구축하는 maxHeaplify()라는 함수가 있다고 가정하고 어떻게 연산을 하는 지 알아보자.
- 현재 노드와 자식 노드의 값을 비교한다.
- 현재 노드의 값이 가장 크지 않으면 자식 노드 중 가장 큰 값과 현재 노드의 값을 바꾼다.
- 만약 자식 노드가 없거나 현재 노드의 값이 가장 크면 연산을 종료한다.
- 맞바꾼 자식 노드의 위치를 현재 노드로 하여 위의 과정을 반복한다.
- 현재 노드와 자식 노드의 값을 비교한다.
📄
힙을 구축할 때는 자식 노드가 없으면 아무런 동작도 하지 않으므로 N부터 힙 구축을 시작하지 않아도 된다. 현재 노드 인덱스가 N/2을 넘으면 자식 노드의 인덱스가 N을 넘는다. 힙의 크기는 N이므로 실제 노드의 인덱스가 N 이상 넘어가는 일은 없으므로 고려하지 않아도 괜찮다.
- 힙 구축은 N이 아니라 N/2부터 시작해도 괜찮다.
- 힙 정렬 과정 : 최대힙
- 최대힙에서 힙 정렬은 루트 노드가 가장 큰 값이므로 루트 노드의 값을 빼서 저장하기만 하면 된다. 다만 루트 노드의 값을 뺀 이후 최대힙을 유지하는 것이 중요하다.
- 정렬되지 않은 데이터로 최대힙을 구축한다.
- 현재 최대힙의 루트 노드와 마지막 노드를 맞바꾼다. 맞바꾼 뒤 마지막 노드는 최대힙에서 제외한다.
- 현재 최대힙은 마지막 노드가 루트 노드가 되었다. 따라서 최대힙을 다시 구축해야 하기 때문에, maxHeapify(1)을 진행하여 최대힙을 구축하고 위의 과정을 다시 수행한다. 이 과정을 최대힙의 크기가 1이 될 때까지 반복한다.
- 최대힙에서 힙 정렬은 루트 노드가 가장 큰 값이므로 루트 노드의 값을 빼서 저장하기만 하면 된다. 다만 루트 노드의 값을 뺀 이후 최대힙을 유지하는 것이 중요하다.
- 힙 정렬의 시간 복잡도
- 정렬되지 않은 값 N개를 힙으로 나타내면 높이가 logN인 트리가 된다. 데이터는 N개이므로 각 데이터에 대해 힙 정렬을 수행하면 시간 복잡도는 O(NlogN)이다.
우선순위 큐
- 우선순위 큐는 우선순위가 높은 데이터부터 먼저 처리하는 큐이다. 쉽게 말해 큐는 큐인데 우선순위에 따라 팝을 하는 큐인 것.
- 우선순위 큐의 내부동작은 힙과 매우 유사하므로 우선순위 큐를 구현할 때는 힙을 활용하는 것이 효율적이다. 여기를 다 공부하면 우선순위 큐 자체가 정렬과 연관이 있음을 알게 된다.
- 우선순위 큐 동작 과정
- 우선순위 큐의 우선순위 기준은 작은 값일수록 우선순위가 높다고 가정
- 빈 우선순위 큐를 하나 선언
- 3을 삽입한다. 빈 큐이므로 별다른 우선순위를 생각하지 않고 맨 앞에 푸시한다.
- 이어서 1을 삽입한다. 1은 3보다 작으므로 우선순위가 높다. 따라서 1을 3으로 삽입한다. 이렇게 하면 3보다 1이 먼저 pop 될 것이다.
- pop을 수행하면 1이 나온다.
- 우선순위에 따라 데이터를 pop할 수 있으므로 정렬과 깊은 연관이 있다는 것도 알았을 것이다.
- 우선순위 큐의 우선순위 기준은 작은 값일수록 우선순위가 높다고 가정
- 힙으로 우선순위 큐를 구현해야 하는 이유
- 우선순위 큐의 핵심 동작은 우선순위가 높은 데이터를 먼저 팝하는 것
- 이를 위해 앞서 언급했던 것처럼 데이터를 푸시할 때마다 아무 정렬 알고리즘을 사용해서 데이터를 우선순위에 맞게 정렬해도 된다.
- 하지만 최소힙이나 최대힙은 특정 값을 루트 노드에 유지하게 하는 특징이 있고, 이는 우선순위 큐의 핵심 동작과 맞아 떨어지므로 힙을 활용하면 우선순위 큐를 효율적으로 구현할 수 있다는 것을 알 수 있다.
- 자바스크립트에서는 힙을 공식적으로 제공하지 않는다.
- 우선순위 큐가 활용되는 분야
- 우선순위 큐는 데이터의 중요성 혹은 우선순위에 따라 처리해야 하는 경우 많이 활용된다.
- 작업 스케줄링
- 응급실 대기열
- 네트워크 트래픽 제어
- 교통 네트워크 최적화
- 우선순위 큐는 데이터의 중요성 혹은 우선순위에 따라 처리해야 하는 경우 많이 활용된다.
위상 정렬
- 일의 순서가 있는 작업을 순서에 맞춰 정렬하는 알고리즘
- 위상 정렬은 일의 순서가 중요하므로 반드시 간선의 방향이 있어야 한다.
- 만약 그래프에 순환이 있거나 간선의 방향이 없으면 일의 방향이 없는 것이므로 방향 비순환 그래프 (Directed Acyclic Graph)에서만 사용할 수 있다.
- 위상 정렬과 진입차수
- 위상 정렬은 자신을 향한 화살표 개수를 진입차수로 정의하여 진행한다.
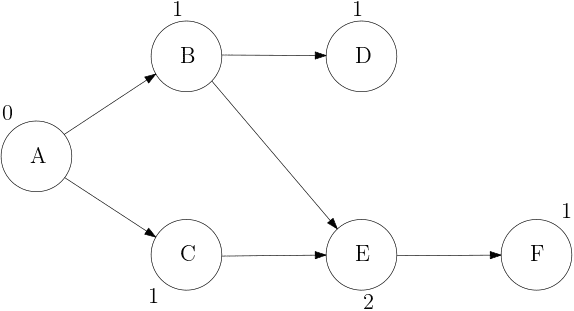
- 진입차수가 0이라고 하면 자신을 향한 화살표가 없다는 뜻이므로 ‘선행 작업이 필요 없는, 바로 할 수 있는 일’이라는 뜻과 같다.
- 위상 정렬은 자신을 향한 화살표 개수를 진입차수로 정의하여 진행한다.
- 위상 정렬 과정
- 위상 정렬은 기본적으로 바로 진행할 수 있는 일, 다시 말해 진입차수가 0인 일을 해결하고 관련된 작업의 진입차수를 1씩 낮추면서 새롭게 진입차수가 0이 된 작업들을 해결하는 식으로 진행한다.
- 이 해결이라는 행위는 큐를 활용하여 구현한다.
- 진입차수가 0인 작업을 일단 전부 큐에 넣고 하나씩 팝하면서 해당 작업과 연결되어 있는 작업들의 진입차수를 줄이고 진입차수가 0이 된 작업을 큐에 넣는다.
- 위상 정렬을 진행할 그래프가 있으면 앞서 말한대로 진입차수를 노드에 작성한다.
- 진입차수가 0인 노드를 큐에 푸시한다. 그런 다음 팝을 하면서 인접한 노드의 진입차수를 -1한다.
- 노드들이 모두 푸시 후 팝 작업이 완료되면 팝한 순서를 늘어놓는다.
- 위상 정렬의 시간 복잡도
- 위상 정렬은 모든 정점과 간선을 딱 한 번씩만 지나므로 시간 복잡도는 O(|V| + |E|)가 된다.
계수 정렬
- 데이터에 의존하는 정렬 방식이다.
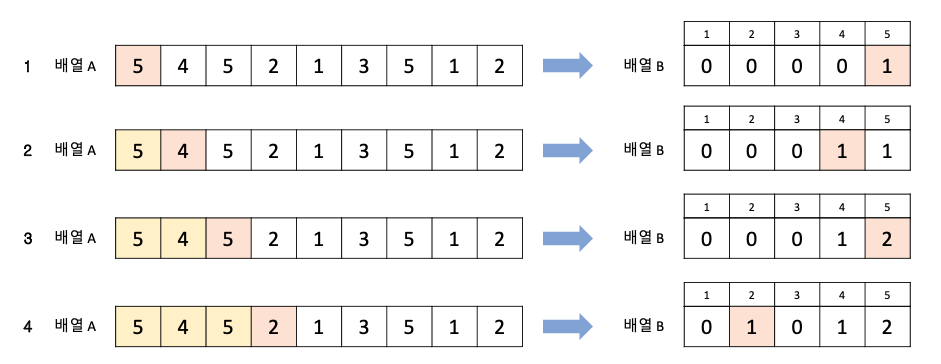
- 지금까지 배운 정렬들은 사용자가 정한 기준에 따라 정렬했다. 반면 계수 정렬은 데이터의 빈도수로 정렬한다.
- 왼쪽의 배열에서 데이터의 빈도수를 세어 빈도수 배열에 저장한 것
- 빈도수를 다 채운 다음 우선 순위가 높은 데이터부터 빈도수만큼 출력하는 것이 계수 정렬
- 계수 정렬의 한계
- 계수 정렬의 핵심 동작은 앞서 본 것처럼 빈도수를 세어 빈도수 배열에 저장하는 것. 그래서 빈도수 배열에 저장할 값의 범위가 듬성듬성 있거나 음수가 있으면 계수 정렬을 하기 곤란하다.
- 계수 정렬의 시간 복잡도
- 값이 N개인 데이터에서 데이터를 세는 과정은 전체 데이터를 한 번씩 체크하면 되므로 N번 탐색한다고 생각할 수 있다.
- 값의 최솟값 ~ 최댓값 범위 크기가 K라면 빈도수 배열에서 K + 1만큼 탐색해야 하므로 계수 정렬의 시간 복잡도는 O(N + K) 라고 생각할 수 있다.
- 정렬 알고리즘의 시간 복잡도정렬 방법 최악의 경우 최선의 경우 특이점
삽입 정렬 O(N^2) O(N) 데이터가 거의 정렬되어 있을 때는 최고의 성능 발휘 병합 정렬 O(NlogN) O(NlogN) 안정적인 성능으로 정렬 가능 병합 과정에서의 추가적인 메모리 필요 힙 정렬 O(NlogN) O(NlogN) 안전적인 성능으로 정렬 가능 데이터를 삽입과 동시에 빠르게 정렬할 수 있다 계수 정렬 O(N + K) O(N + K) 데이터에 의존적이므로 항상 사용 가능한 것은 아님 위상 정렬 O(V + E) O(V+E) 작업의 순서가 존재할 때 사용되는 알고리즘 - N은 원소의 길이, K는 원소값의 범위, V는 정점, E는 간선의 개수
- 정렬이 안정적이다?
- 성능이 안정적이라는 뜻이 아니라 동일한 우선순위를 가진 원소들의 상대적 순서가 정렬 후에도 보존되는 것을 말한다.
문제 풀이
-
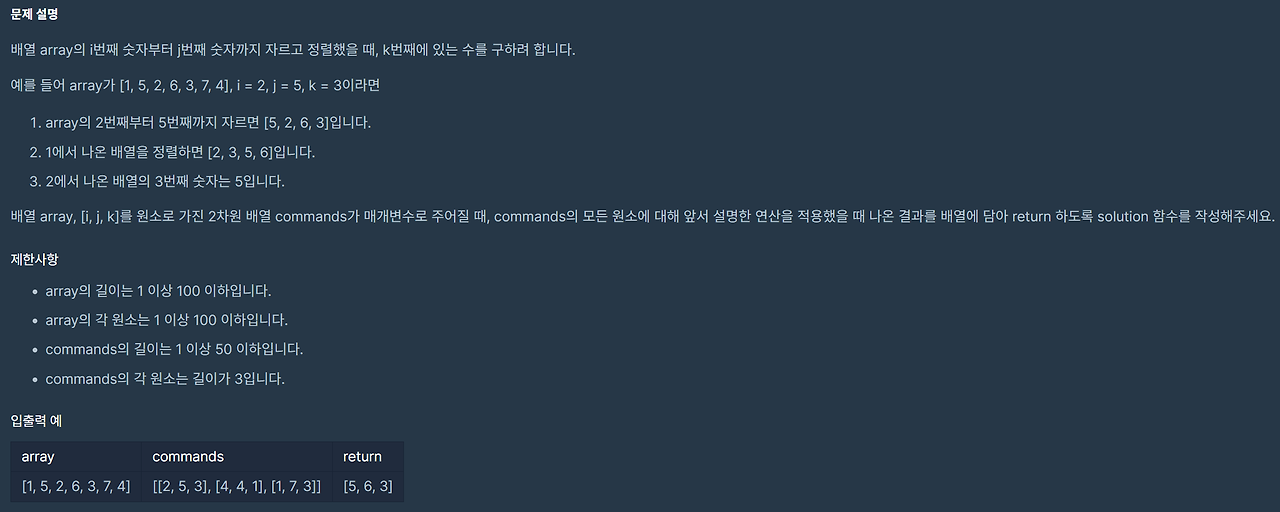
- K번째 수
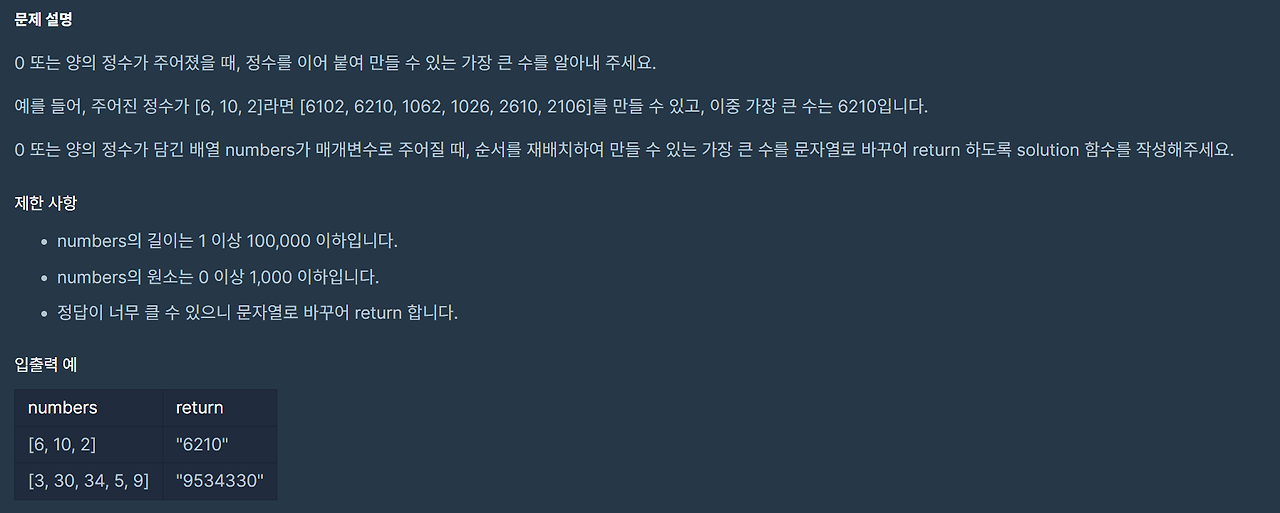
- 가장 큰 수
- H - index

출처
- 코딩테스트 합격자 되기 - 자바스크립트 편
'알고리즘' 카테고리의 다른 글
| [알고리즘 고득점 kit] 힙 (개념, 문제풀이) (0) | 2024.09.19 |
|---|---|
| [알고리즘 고득점 kit] 스택 / 큐 (개념, 문제풀이) (0) | 2024.09.15 |
| [알고리즘 고득점 kit] 해시 (개념, 문제풀이) (0) | 2024.09.06 |

